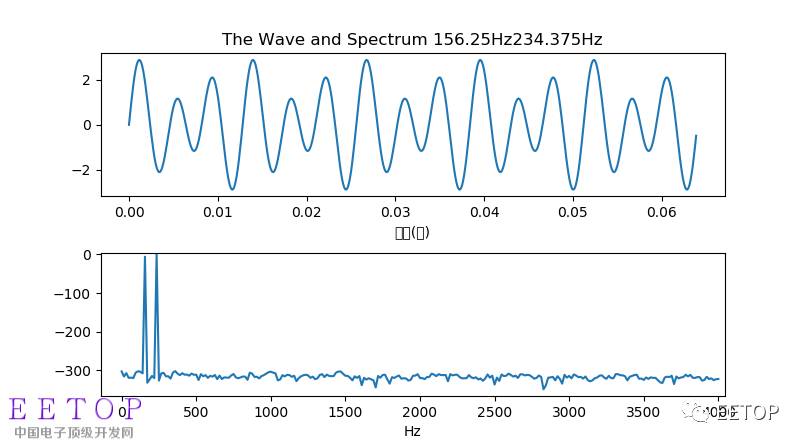
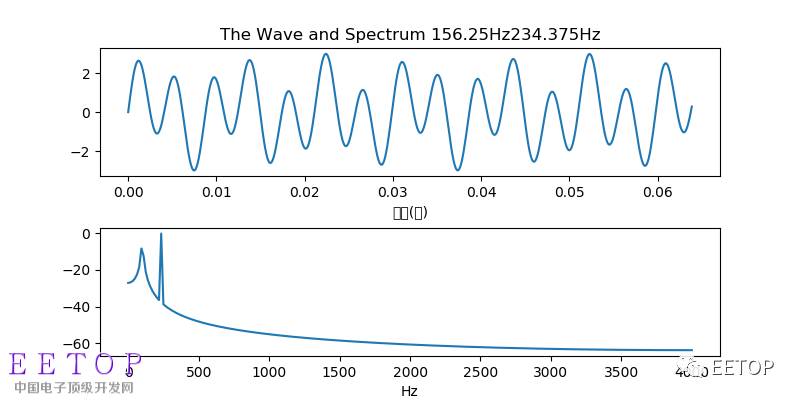
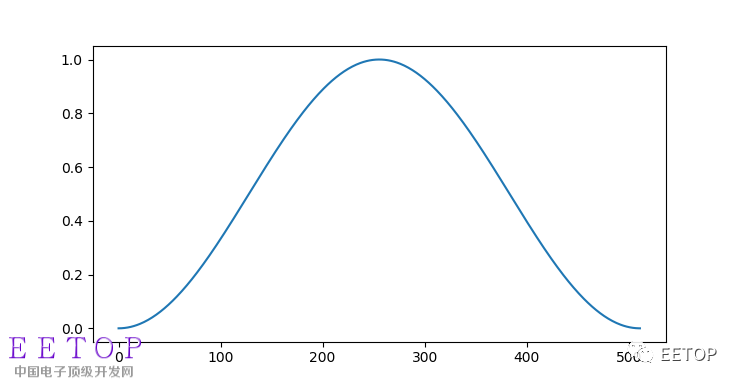
Python is the current hot language. I always feel that mastering a programming language is still necessary for technology. Combining some data processing and analysis that can be used in the work, I feel that I can start with data analysis and strive for Master some of Python's applications in data processing. The following is an introduction to the spectrum analysis of digital signals based on Python numpy. Fourier transform is a bridge between the time domain and the frequency domain in the signal domain. It is more convenient to perform some analysis in the frequency domain. Fourier is mainly aimed at the analysis of the frequency characteristics of stationary signals. Simply speaking, it is a signal with a certain periodicity. Because the Fourier transform adopts the method of limited sampling, there are certain requirements for the sampling length and sampling objects. # _*_ coding:utf-8 _*_ Import numpy as np #import a data processing module Import pylab as pl #import a drawing module, module under matplotlib Sampling_rate = 8000 ##sampling frequency Fft_size =512 #FFT processing sample length t = np.arange(0,1.1,1.0/sampling_rate) #np.arange (starting point, end point, interval) produces a sampling time of 1 s long x = np.sin(2*np.pi*156.25*t)+2*np.sin(2*np.pi*234.375*t) #Two sine wave superposition, 156.25HZ and 234.375HZ, so as simple as above # Introduction FFT has requirements for sampling time, The requirement for accurate spectral analysis of the #N point FFT is that N sampling points contain an integer number of # Waveform of the sampled object. # Therefore, the N-point FFT can perfectly calculate the spectrum requirements for sampling objects. #是n*Fs/N(n*sampling frequency/FFT length), # Therefore for 8KHZ and 512 points, #The minimum requirement for the perfect sampling object is 8000/512=15.625HZ, # Therefore 156 of 156.25 is 10, and n of 234.375 is 15. Xs = x[:fft_size]# Sampling fft_size points from waveform data for operation Xf = np.fft.rfft(xs)/fft_size # FFT calculation using np.fft.rfft(), rfft() is for more convenience #Transform the real number signal, the formula knows /fft_size in order to correctly display the waveform energy The return value of the #rfft function is N/2+1 complex numbers, representing 0 (Hz) respectively. #到sampling_rate/2(Hz) points. #以是, The following np.linspace can be used to calculate the true frequency corresponding to each subscript in the return value: Freqs = np.linspace(0,sampling_rate/2,fft_size/2+1) # np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None) # Returns evenly spaced numbers within the specified interval Xfp = 20*np.log10(np.clip(np.abs(xf),1e-20,1e1000)) # Finally we calculate the amplitude of each frequency component and pass 20*np.log10() # Convert it to a value in db units. In order to prevent the 0-value component from causing log10 to be calculated, #we call np.clip to perform upper and lower limits on the amplitude of xf Pl.figure(figsize=(8,4)) Pl.subplot(211) Pl.plot(t[:fft_size], xs) Pl.xlabel(u"time (seconds)") Pl.title(u"The Wave and Spectrum 156.25Hz234.375Hz") Pl.subplot(212) Pl.plot(freqs, xfp) Pl.xlabel(u"Hz") Pl.subplots_adjust(hspace=0.4) Pl.show() #绘图Show results Now let's take a look at the spectrum leakage and change the frequency of the sampled object. x = np.sin(2*np.pi*100*t)+2*np.sin(2*np.pi*234.375*t) We clearly see that the spectrum analysis of the first object is “leaked†and the energy is dispersed to other frequencies. It is impossible to accurately calculate the spectral characteristics of the calculated object. Window function As we can see above, we can deal with it by adding the "window" function, try to ensure the FFT length The sampling object is symmetrical. Import pylab as pl Import scipy.signal as signal Pl.figure(figsize=(8,3)) Pl.plot(signal.hann(512))# Hamming window function Pl.show() The windowing process is performed on the above-mentioned function of spectrum leakage, and the principle and effect of various windowing functions will be introduced later. Class 2 Power Adapter 12V,Switching Adapter 12V,12 Volt Power Adapter,12V Class 2 Power Adapter ShenZhen Yinghuiyuan Electronics Co.,Ltd , https://www.yhypoweradapter.com